Walsh Synthesis
Only from XXth century, almost young.
Antique or not? Forgotten and overcome by technological progress.
What is Walsh Synthesis?
A forgotten sound synthesis technique. A bit short you say? OK, let's go.
A bit of history...
All begins with Fourier, Joseph was his first name, a french guy, who discovered around 1820 that all signals can be decomposed by sums of sines. If you like maths, here's the Wikipedia link. Of course, at this time it was not a question about sound synthesis but about physical phenomena, heat for exemple. It's way later his formulas were used for sound synthesis, mainly by his famous FFT (Fast Fourier Transform). With computers it was time to convert continuous signal to discrete ones. By discrete I mean step by step.
Around 1920 Joseph Walsh, américain, had an eye on Fourier transform and discovered that if a signal can be a sum of sines it can be as well a sum of binary signals, in other terms a sum of square waves. His discovery, with the help of the french Hadamard was the born of what is called today FWT (Fast Walsh Transform). Note that some help was given by a German called Rademacher, well known in maths. If you're interested by details, go to this Wikipedia link.
In the free and open-source GNU Octave, you won't find the Walsh function but the Hadamard one. Results are the same except the order of the series.
Exemple: >> hadamard(8)
ans =
1 1 1 1 1 1 1 1 Walsh 0
1 -1 1 -1 1 -1 1 -1 Walsh 7
1 1 -1 -1 1 1 -1 -1 Walsh 3
1 -1 -1 1 1 -1 -1 1 Walsh 4
1 1 1 1 -1 -1 -1 -1 Walsh 1
1 -1 1 -1 -1 1 -1 1 Walsh 6
1 1 -1 -1 -1 -1 1 1 Walsh 2
1 -1 -1 1 -1 1 1 -1 Walsh 5
The order of Walsh's functions is based on the sign changes. Why is it pertinent?
When the first computers began to appear, they stood out mainly for the space they took up, their weight and their prohibitive price, not for their power. It got better time after time and we finally arrived at the first personal computers. Immediately one wanted to produce music on these machines but how to make listenable music on a 8 bit machine with 8 Ko of memory? How to use sine tables, superimpose and call them? Sine table are composed of real numbers, not integers or binary ones, big problem at that time. An other problem is the computing power. To get a clean sine table you need at least 256 sines to be barely listenable by a human ear. Here came the clearing for the Walsh synthesis. This technique only uses binary numbers, 0 or 1. If it's -1 just use 0. 0 = Off, 1 = On, easy. Better, with only 16 tables made by 16 binary numbers, 15 tables if you skip the first one, we obtain a completely listenable sound. It was the perfect formula to make music even on an Amstrad or on an Oric. A time that those under 30 cannot know... Before the emergence of the first personal computers, this type of synthesis had been pioneered on slightly more powerful and much larger computers., even the IRCAM was interested in this synthesis. Making these Walsh series was easy with the logic gates that are at the heart of microprocessors, it seemed the future of computer sound synthesis. But the clearing was short-lived.
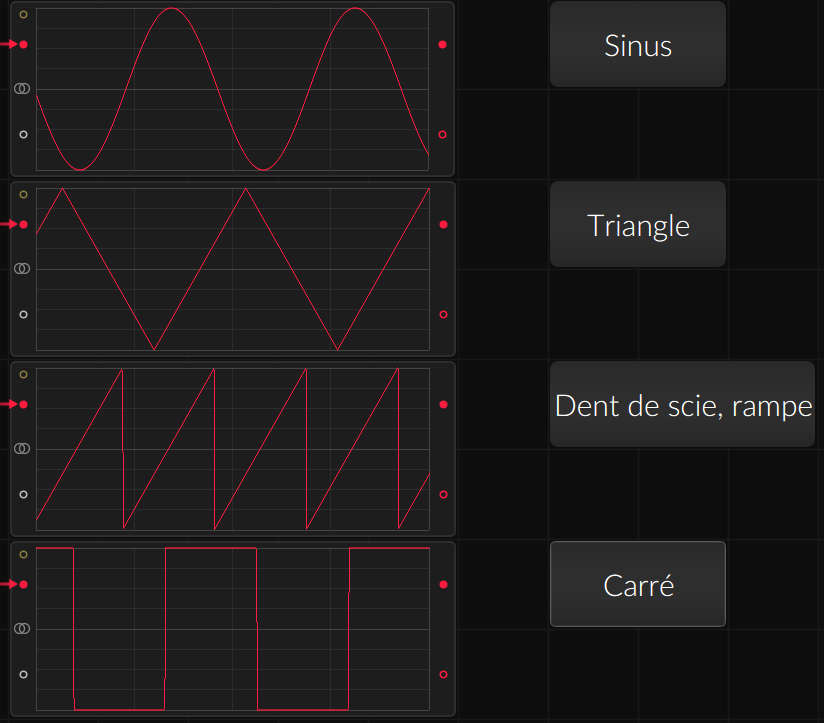
There are four wave shapes to create a sound
It's possible with only square waves. Exemple here with the 8 iterations of Walsh(8)
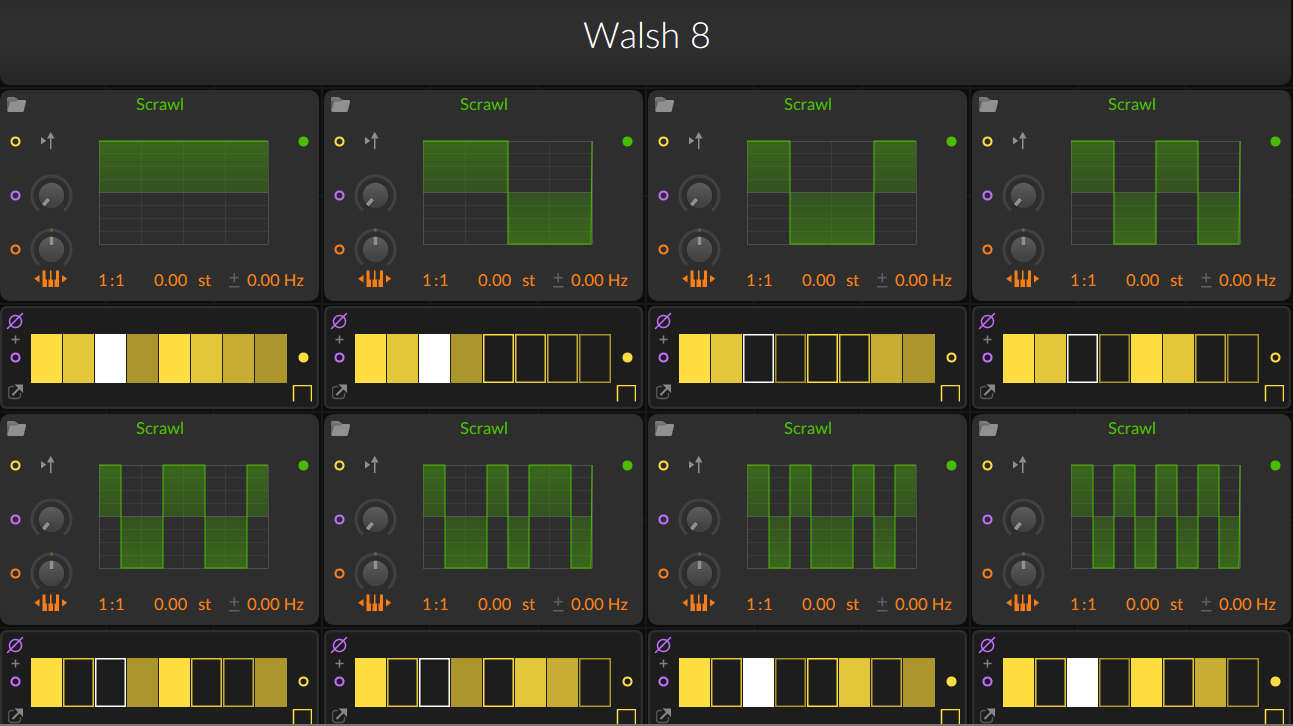
Green: data with 1 and -1. Yellow: binary values.
Note the first graph, all values are 1. Addition makes no change to the shape of the resulting wave, only to its overall volume. The 1st iteration is therefore useless and is not used, you'll just have to adjust the final volume. Also note that all iterations fit in one byte, i.e. a sequence of 8 bits. This means that the very essence of the sound engine which would use this synthesis would only need 15 bytes as a database. A ZX81 was largely capable of it in 1981, even the iconic RCA Cosmac VIP could. But there are still two problems. The first, which IRCAM, although at the forefront of musical research, has not been able to get around: harmonics
The harmonics of the sinusoids give pitches (musical tones) linked to mathematics. The basic harmonic, the fundamental, sets a tone. The second harmonic (frequency multiplied by 2) will give a doubled pitch, i.e. the frequency multiplied by 2, in other words the tone passed to the higher octave. Example, a fundamental sinusoid of 440 Hz (A 4) has a second harmonic of 880 Hz (A 5). The fourth harmonic will give a pitch at 1760 Hz, (A 6). What's going on with the harmonics of the Walsh series? Nothing like that... The frequency does not follow the order of the harmonics. Not so simple then?
2nd and last, the most fatal: The arrival of 16-bit computers and compact discs. The speed of evolution of computers has made obsolete the frantic search to stick as closely as possible to the architecture of microprocessors. Any desktop or personal computer could very quickly calculate an FFT and its memory was not at all impressed by the few kilobytes required for a sine wave table even when encoded in real numbers. The arrival of the CD format was the final blow, computers and the music industry were both based on 16-bit format with a sampling frequency of 44.1 KHz. From then on Fourier had won the battle.
What remains of Walsh's synthesis? One synthesizer, just one, the unique RMI Harmonic Synthesizer. It used 2 generators of 16 Walsh sequences, was manufactured in 200 copies and was sold in only 6 copies, including 1 to Jean Michel Jarre. There is very little authentic documentation regarding this rarity. Ahead of its time, stuck between analog synthesis and digital synthesis based on well-established knowledge, this synthesis barely had time to see the light of day before it was obsolete.
A patch for Bitwig (Not a free software) to test Walsh synthesis: here (soon)
A patch for VCV Rack (Free software) to test Walsh Synthesis: here
If you type "Walsh synthesis" into Google you only find results in English. If you know a reference in French I am interested, my address is at the bottom of the page. In English there are 3 essential references:
Owen Brown's article: A Digital Waveform Synthesizer Using Walsh Functions
A special issue of Byte Magazine dedicated to music published in 1979 available here: The Byte book of computer music
And the article by two engineers who firmly believed in it, Goffredo Haus and Mario Malcangi: Portable Walsh Synthesizer.
The essential "Experimental Electronic Music Device Employing Walsh Functions" by Bernard A. HUTCHINS Jr. available here
By searching a little with your friend Google you will find other documents but nothing in French.
