Synthèse de Walsh

Qu'est-ce que la synthèse de Walsh?

Une forme de synthèse sonore oubliée. C'est un peu court jeune homme, mais encore?

Un peu d'histoire des synthèses sonores.

Tout commence avec Fourier, Joseph de son prénom, français, qui découvrit dans les années 1820 que n'importe quel signal peut être décomposé en une somme de sinusoïdales. Pour les férus de mathématiques, voici le lien Wikipédia de la chose. Il n'était alors évidemment pas question de synthèse musicale mais de phénomènes physiques, notamment la chaleur. C'est bien plus tard que ses formules furent utilisées en synthèse sonore, entre autres par sa formule désormais célèbre, la transformée de Fourier. Avec l'avènement de l'informatique et du traitement de signal il fallait transformer le phénomène physique continu en phénomène discret. Pas à pas ou étape par étape pour faire simple. Arriva donc la transformée rapide de Fourier couramment appelée FFT (Fast Fourier Transform).

Dans les années 1920 Joseph Walsh, un américain, se pencha sur la transformée de Fourier et découvrit qu'un signal est certes la somme de sinusoïdales mais qu'il peut également être décomposé en signaux binaires, autrement dit en ondes carrées. Il découvrit les fonctions de Walsh puis après études conjointes avec Hadamard, français, ils mirent au point la transformée rapide de Walsh-Hadamard, cette fois appelée "affectueusement" FWT (Fast Walsh Transform). N'oublions pas dans la foulée les travaux de l'allemand Hans Rademacher qui simplifia pas mal les travaux de Walsh. Pour les fans de mathématiques, voici le lien Wikipédia.

Dans le programme gratuit et open-source GNU Octave, vous ne trouverez pas la fonction de Walsh mais la fonction d'Hadamard. Le résultat des deux est similaire, seul change l'ordre des résultats.

Exemple: >> hadamard(8)

ans =

1 1 1 1 1 1 1 1 Walsh 0

1 -1 1 -1 1 -1 1 -1 Walsh 7

1 1 -1 -1 1 1 -1 -1 Walsh 3

1 -1 -1 1 1 -1 -1 1 Walsh 4

1 1 1 1 -1 -1 -1 -1 Walsh 1

1 -1 1 -1 -1 1 -1 1 Walsh 6

1 1 -1 -1 -1 -1 1 1 Walsh 2

1 -1 -1 1 -1 1 1 -1 Walsh 5

L'ordre des fonctions de Wash est lié uniquement au nombre de changements de signes mais les résultats sont identiques à ce détail près. En quoi c'est pertinent?

Quand les premiers ordinateurs ont commencé à pointer le bout de leur nez ils brillaient surtout par la place qu'ils occupaient, leur poids et leur prix prohibitif, pas par leur puissance. Ca c'est amélioré au fil du temps et on est enfin arrivés aux premiers ordinateurs personnels. Tout de suite l'envie de produire de la musique sur ces machines s'est faite sentir mais comment faire jouer une musique écoutable sur une machine 8 bits avec 8 Kilo octets de mémoire? Comment faire tenir des sinusoidales dans des tables, les superposer et les appeler? Une table de sinusoïdales c'est des nombres réels, pas entiers, premier écueil. L'autre est la puissance de calcul nécessaire pour qu'une somme de sinusoïdales sorte un onde triangulaire propre d'autant qu'il en faut au moins 256 pour être potable à des oreilles humaines. C'est là que l'éclaircie est apparue pour la synthèse de Walsh. Non seulement elle n'utilise que des chiffres binaires (0 et 1 parce que le -1 des résultats a été assimilé à 0) et avec 16 tables (et même 15 en pratique) de 16 chiffres on obtient des sons tout à fait écoutables. C'était la formule parfaite pour produire de la musique sur ordinateurs, même sur un Oric ou un Amstrad. Un temps que les moins de 20 ans etc etc... Avant que n'émergent les premiers ordinateurs personnels ce type de synthèse avait été défriché sur des ordinateurs un peu plus puissants et beaucoup plus imposants, même l'Ircam s'était intéressé à cette synthèse. Fabriquer ces séries de Walsh était facile avec les portes logiques qui sont au cœur des microprocesseurs, ça semblait l'avenir de la synthèse sonore par ordinateur. Mais l'éclaircie fut de courte durée.

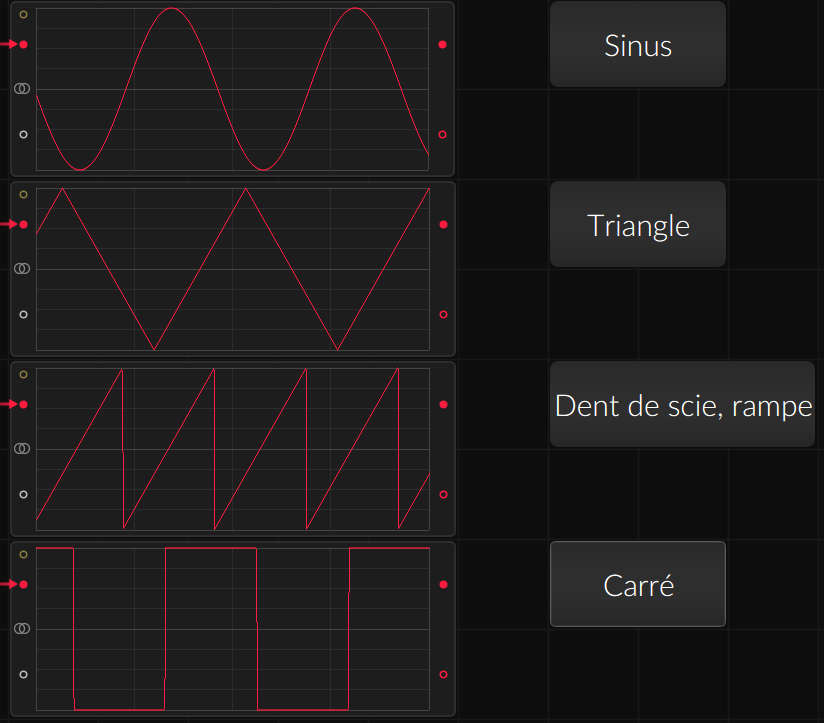
Il existe 4 formes d'onde de base pour former un son

Avec seulement des ondes carrées on peut le faire. Exemple avec les 8 itérations de Walsh(8)

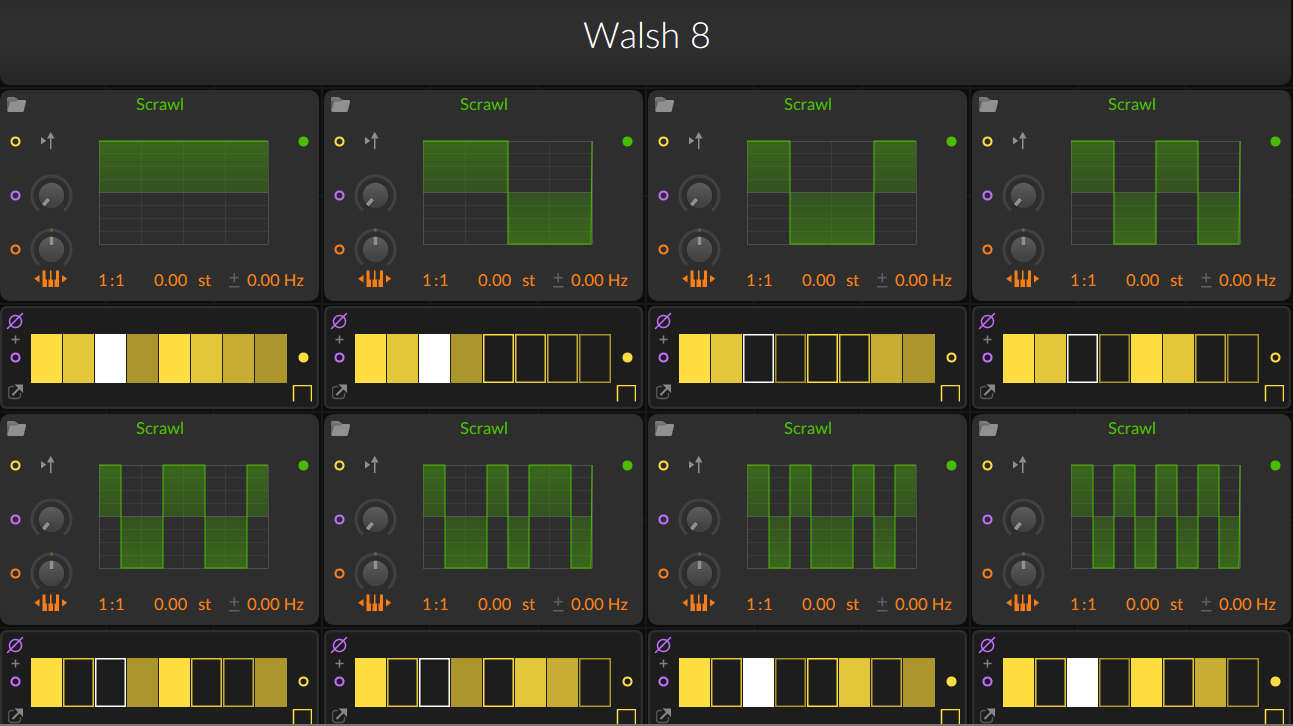
En vert les données de -1 à 1, en jaune les valeurs binaires

Notez le premier graphique, toutes les valeurs sont à 1. L'addition (ou la soustraction) n'apporte aucun changement à la forme de l'onde résultante, seulement à son volume global. La 1ère itération ne sert donc à rien et n'est pas utilisée, il suffit de régler le volume final. Notez également que toutes les itérations tiennent dans un octet, soit une suite de 8 bits. Ca signifie que l'essence même du moteur sonore qui utiliserait cette synthèse n'aurait besoin que de 15 octets comme base de données. Un ZX81 en était largement capable en 1981, même l'iconique RCA Cosmac VIP le pouvait. Mais il y a un mais, il y en a même deux. Le premier, que l'Ircam pourtant à la pointe de la recherche musicale n'a pas pu contourner:

Les harmoniques des sinusoïdes donnent des pitchs (tons musicaux) liés aux mathématiques. L'harmonique de base, la fondamentale, donne un ton. La seconde harmonique (fréquence multipliée par 2) donnera un pitch double, soit la fréquence multipliée par 2, autrement dit le ton passé à l'octave supérieure. Exemple, une sinusoïde fondamentale de 440 Hz (La 4) a une seconde harmonique de 880 Hz (La 5). La quatrième harmonique donnera un pitch à 1760 Hz, (La 6). Que se passe t-il avec les harmoniques de la série de Walsh? Rien de tel... La fréquence ne suit pas l'ordre des harmoniques. Pas si simple alors?

2ème et dernier mais, le plus fatal: L'arrivée des ordinateurs 16 bits et des compacts discs. La rapidité d'évolution des ordinateurs a rendu obsolète la recherche effrénée de coller au plus près de l'architecture des microprocesseurs. N'importe quel ordinateur de bureau ou de salon a très rapidement pu calculer une FFT et sa mémoire n'était pas du tout impressionnée par les quelques kilooctets nécessaires à une table d'ondes sinusoïdales même codée en nombres réels. L'arrivée du format CD a été le coup fatal, les ordinateurs et l'industrie musicale étaient tous deux basés sur du format 16 bits avec une fréquence d’échantillonnage de 44,1 KHz. Dès lors Fourier avait gagné la bataille.

Que reste t-il de la synthèse de Walsh? Un synthétiseur, un seul, le RMI Harmonic Synthesizer. Il utilisait 2 générateurs de 16 séquences de Walsh, aurait été fabriqué à 200 exemplaires et aurait été vendu à 6 exemplaires seulement, dont 1 à Jean Michel Jarre. Il y a très peu de documentation authentique concernant cette rareté. En avance sur son temps, coincée entre la synthèse analogique et la synthèse numérique basée sur des connaissances bien établies, cette synthèse a à peine eu le temps d'ouvrir l’œil qu'elle était obsolète.

Un patch Bitwig (Programme payant) pour tâter de la synthèse de Walsh: ici

Un patch VCV Rack (Programme gratuit) pour tâter de la synthèse de Walsh: ici

Si vous tapez "synthèse de Walsh" dans l'ami Google vous ne trouvez que des résultats en anglais. Si vous connaissez une référence en français je suis preneur, mon adresse est en bas de la page. En anglais il n'y a que 4 références qui sont incontournables:

• L'article de Owen Brown: A Digital Waveform Synthesizer Using Walsh Functions

• Un numéro spécial de Byte Magazine consacré à la musique publié en 1979 disponible ici: The Byte book of computer music

• J'en tente une traduction sur cette page.

• Et l'article de deux ingénieurs qui y croyaient dur comme fer, Goffredo Haus et Mario Malcangi: Portable Walsh Synthesizer.

• L'incontournable "Experimental Electronic Music Device Employing Walsh Functions" par Bernard A. HUTCHINS Jr. disponible ici

En fouillant un peu avec l'ami Google vous trouverez d'autres documents mais rien de rien en français.