Traduction vite faite de l'article de Byte Magazine.
À l'aide d'une technique mathématique appelée analyse de Fourier, il est possible de créer des formes d'onde arbitraires en additionnant divers «composants».
Bien qu'une pleine appréciation du fonctionnement interne de la série de Fourier nécessite une connaissance des mathématiques avancées bien au-delà des capacités de nombreuses personnes intéressées par l'électronique, cela ne les dissuade en aucun cas d'utiliser les concepts ou même des parties simplifiées des mathématiques dans des applications pratiques. Même les débutants savent que les formes d'onde peuvent être divisées en un ensemble d'harmoniques et qu'un ensemble d'ondes sinusoïdales de fréquences multiples entières peut être additionné pour construire une forme d'onde complexe. De la même manière, les concepts de fonctions de Walsh peuvent être mis en œuvre dès que quelques idées fondamentales sont maîtrisées. La clé pour générer des sons complexes dans les sorties musicales et vocales informatisées est la capacité à générer des formes d’ondes arbitraires à partir de codes numériques.
À l’heure des ordinateurs numériques, une personne familiarisée avec les concepts de Fourier pourrait se poser la question: est-il possible de créer n’importe quelle forme d’onde à partir d’une somme d’ondes carrées d’un certain type ? Un tel système serait idéal pour une utilisation avec une logique numérique. Cette question a reçu une réponse affirmative du mathématicien allemand H Rademacher, non pas en 1972 ou 1962, mais en 1922. Son ensemble d'ondes carrées appelé « fonctions Rademacher » consiste en une onde carrée fondamentale d'un rapport cyclique de 50 % à une certaine fréquence plus des harmoniques d'ondes carrées de 2, 4, 8, 16, 32 et des puissances supérieures de deux fois la fréquence fondamentale. Cependant, un défaut de ce système est qu'il n'est pas possible de générer une forme d'onde arbitraire à partir d'une simple somme de ces harmoniques d'onde carrée.
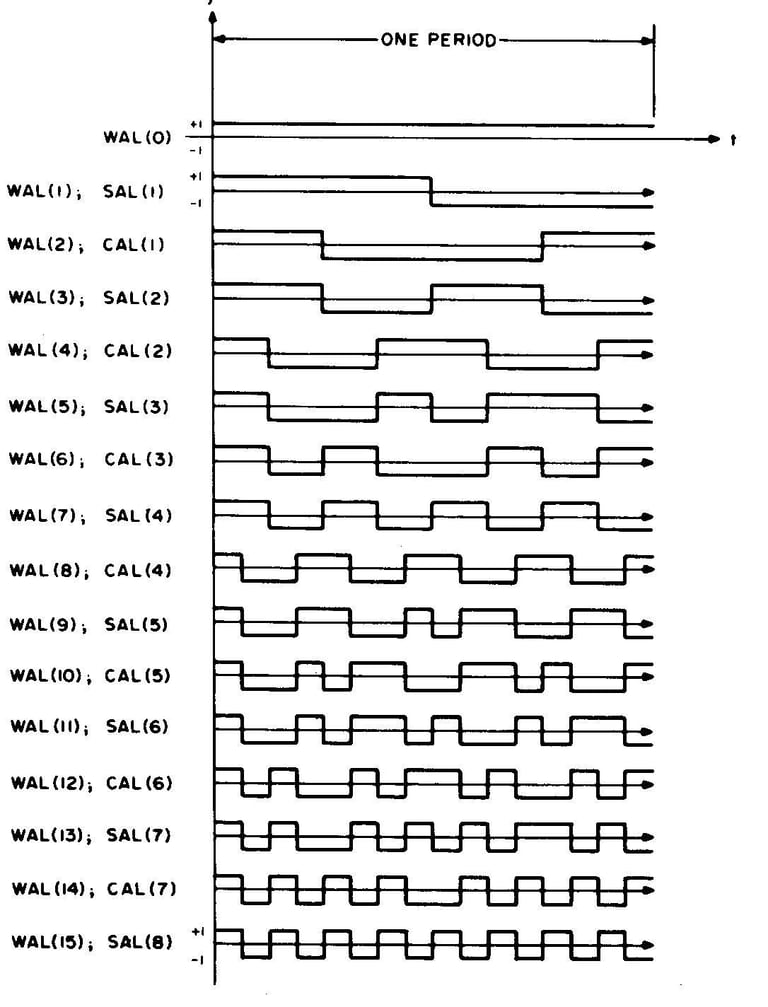
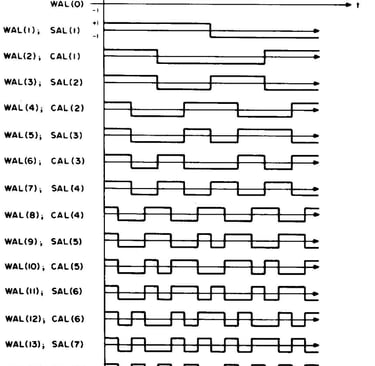
Figure 1 : Les fonctions de Walsh WAL(0) à WAL(15). Le fait que les fonctions de Walsh se prêtent à la génération numérique est évident dans la nature des formes d'onde de base. Les notations SAL et CAL soulignent la ressemblance des fonctions de Walsh avec les fonctions trigonométriques de la série de Fourier SIN et COS.
Figure 2 : La logique d'un circuit numérique qui génère un ensemble de fonctions de Walsh à l'aide d'une chaîne de flip flops et d'un déclenchement externe par gates. Les flip flops sont connectées en bascules (division par 2 à chaque étage). Les portes OU exclusif combinent des termes pour produire les formes de Walsh plus compliquées indiquées.
Les séries de Fourier sont utilisées pour créer des formes d'onde comme la somme d'ondes sinus et cosinus pures à des fréquences sélectionnées; cela nous amène à la question évidente : est-il possible d'utiliser un mécanisme similaire qui construise une forme d'onde complexe à partir de formes d'ondes numériques aux arêtes vives ?
Les fonctions de Walsh sont la réponse aux sinus et cosinus utilisés dans l'analyse de Fourier.
En traduisant une somme mathématique en un circuit physique, l'amplificateur opérationnel fournit l'élément de sommation et les résistances des entrées vers le nœud de sommation qui forme les coefficients du composant signal.
Également en 1922, J. L. Walsh présenta son système développé de manière indépendante à l'American Mathematical Society. Son système a ensuite été revu par le mathématicien polonais Kaczmarz en 1929 pour inclure le système Rademacher comme sous-ensemble de l'ensemble complet de fonctions orthonormées de Walsh, ce qui, en français ordinaire, dit que certaines des fonctions de Walsh sont des ondes carrées et que si toutes les fonctions de Walsh sont autorisées (pas besoin cependant de toutes les utiliser), alors toute forme d'onde périodique arbitraire peut être construite en les utilisant ensemble d'une manière totalement analogue à la sommation sinusoïdale dans les séries de Fourier.
L'intérêt pour les applications techniques des fonctions de Walsh a été suscité par un article sur le IEEE Spectrum du Dr H. F. Harmuth de l'Université du Maryland en 1968 et se poursuit encore aujourd'hui en raison de l'adéquation des fonctions de Walsh à la génération par des systèmes numériques.
Le moyen le plus rapide de comprendre ce que sont les fonctions de Walsh est simplement de regarder une image de certaines formes d'onde. La figure 1 montre les fonctions de Walsh WAL(0) à WAL(15). On voit que WAL(0) est simplement un DC offset que nous ignorerons généralement dans les applications pratiques puisque ces décalages sont facilement gérés par d'autres moyens et que WAL(1) , WAL(3), WAL(7) et WAL(15) sont en réalité les fonctions carrées de Rademacher. Vous remarquerez qu'en plus des désignations WAL(n), les fonctions sont également appelées CAL ou SAL. Ces étiquettes sont également couramment utilisées et sont des acronymes pour les termes Cosinus wALsh et Sinus wALwh par analogie avec l'analyse de Fourier. En bref, tous les WAL(n pair) sont appelés CAL et tous les WAL(n impair) sont appelés SAL. SAL et CAL sont eux aussi numérotés mais les numéros ne correspondent pas à la désignation WAL mais ils sont faciles à retrouver. Par analogie avec l'analyse de Fourier, un spectre de Walsh est appelé spectre de séquence par opposition à spectre de fréquence de Fourier.
Faites entrer M. Gray et son code
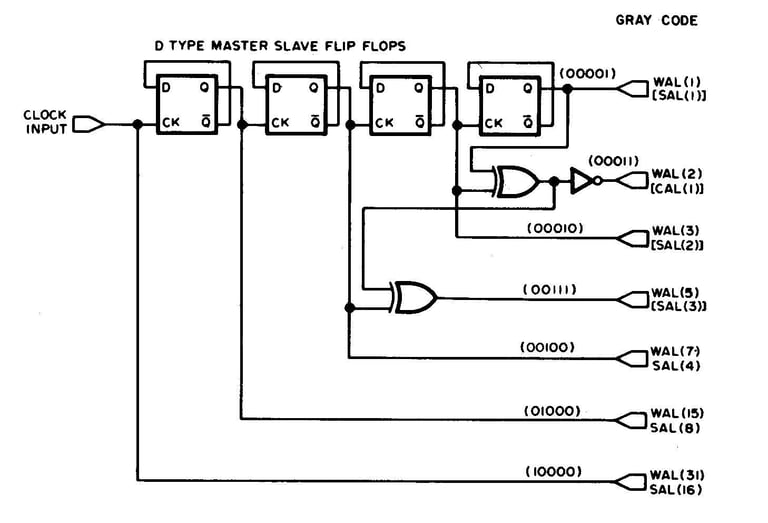
Cependant, savoir à quoi ressemblent les fonctions de Walsh et savoir comment les générer numériquement sont deux choses différentes. Il est clair que la génération de WAL(1), WAL(3), WAL(7), WAL(15), etc., est un jeu d'enfant puisqu'il s'agit de simples ondes carrées. Une chaîne de flip flops (bascules) fait l'affaire, comme le montre la figure 2. La génération des fonctions restantes, bien qu'un peu plus difficile, n'est pas incroyablement complexe une fois que les mathématiques sont réduites à quelques règles simples :
1. Pour générer WAL(n), écrivez d’abord le nombre n en code Gray. Le code Gray est un code binaire modifié dont un seul bit change à la fois lors du passage au nombre immédiatement supérieur ou inférieur. Un tableau de nombres en code Gray est présenté dans le tableau 1 et avec un peu d'étude, le modèle peut facilement être étendu à n'importe quelle valeur.
2. En commençant par le bit le moins significatif (LSB), attribuez une fonction Rademacher à onde carrée à chaque bit. Attribuez WAL(1) au LSB, WAL(3) au suivant, WAL(7) au suivant, etc. Le bit le moins significatif est évidemment celui situé le plus à droite du nombre binaire. Le LSB de 10101000 est donc 0.
3. Toute fonction Rademacher dont le bit est 0 n'est pas utilisée. Celles dont les bits sont à 1 sont combinées par addition modulo 2, c'est-à-dire par des portes OU exclusives pour donner la sortie Walsh de cet ordre.
4. Toutes les fonctions de Walsh doivent commencer positivement, de sorte que la sortie composite de Walsh devra peut-être être inversée en fonction du nombre de portes OU exclusives utilisées pour la produire.
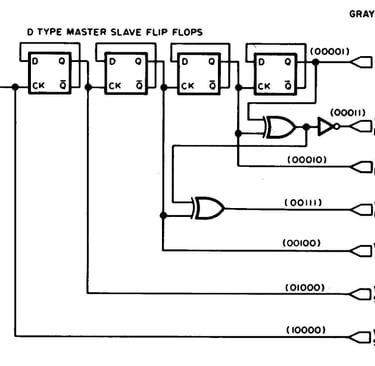
Quelques exemples sont présentés dans la figure 2 et un générateur complet produisant toutes les fonctions de Walsh de WAL(1) à WAL(15) est présenté dans la figure 3.
Il convient de noter que bien qu'une fonction de Walsh soit mathématiquement définie comme allant de +1 à -1, et qu'il soit possible d'obtenir des oscillations positives et négatives par une logique CMOS et des alimentations positives et négatives, en pratique on ne gagne pas grand-chose en suivant cette voie puisque tout ce qui est impliqué est un DC offset qui est facilement géré par l'amplificateur sommateur. Donc, des sorties logiques TTL 0-5 volts conviennent.
Maintenant qu'un ensemble de fonctions de Walsh a été généré, il ne reste plus qu'à les ajouter dans un amplificateur sommateur avec des amplitudes et des signes appropriés pour simuler n'importe quelle forme d'onde avec une approximation en marche d'escalier. L'expression générale d'une représentation de fonction de Walsh est une sommation analogue à celle trouvée dans l'analyse de Fourier.
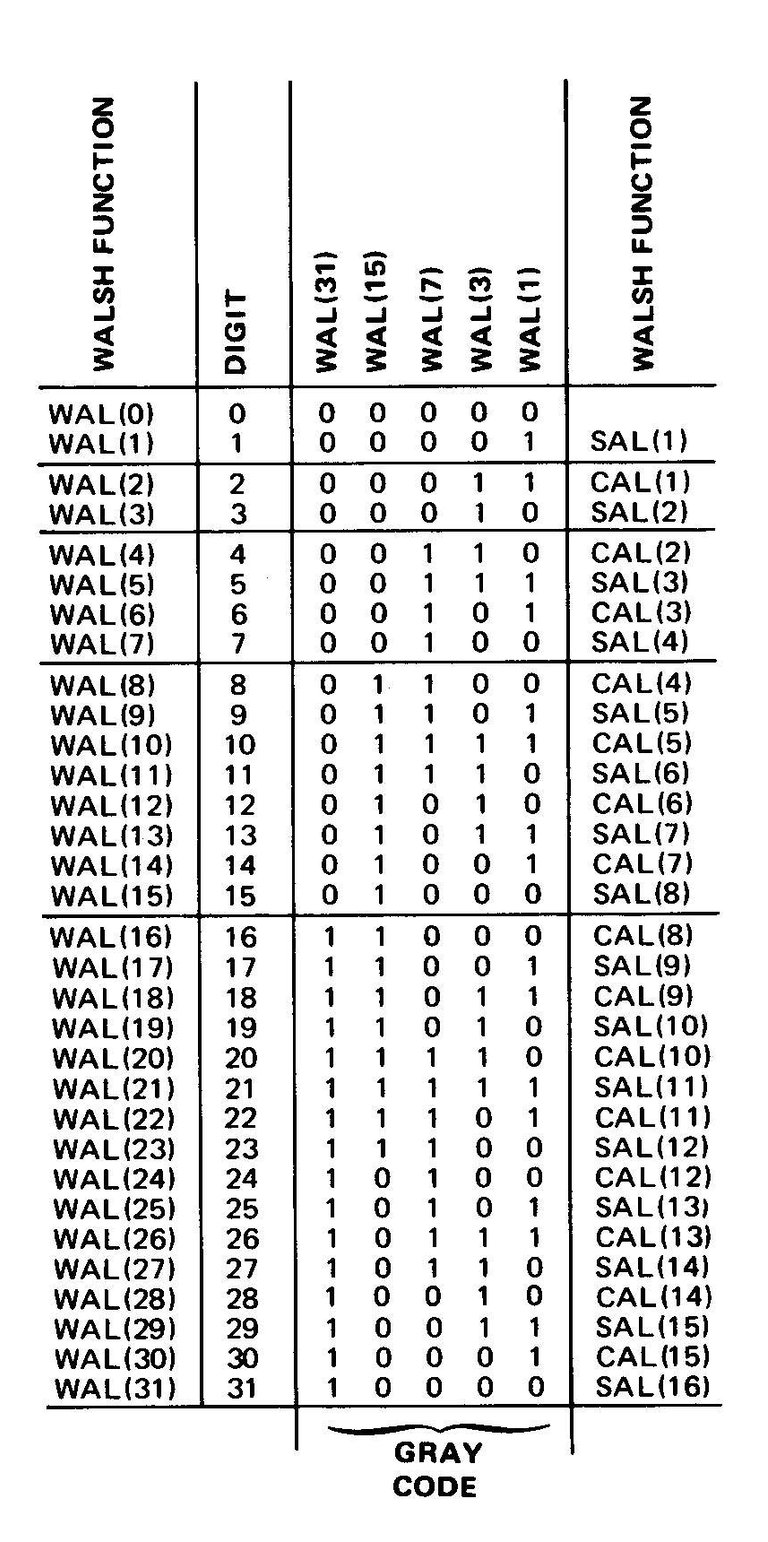
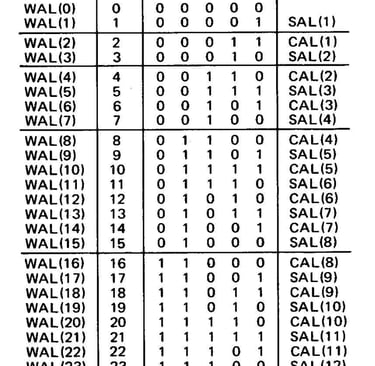
Tableau 1 : Modèles binaires de code Gray pour les fonctions de Walsh WAL(0) à WAL(31). La notation SAL et CAL correspondante de chaque fonction WAL est indiquée dans la colonne de droite du tableau.
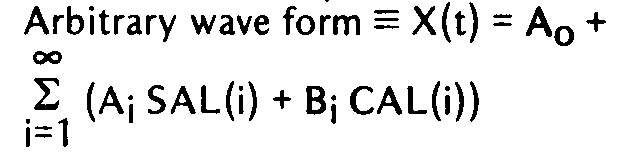
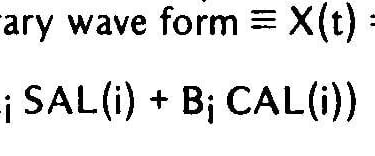
Formule pour une forme d'onde arbitraire
Où Ai et Bi sont des constantes de pondération qui correspondent aux résistances utilisées dans les entrées de l'amplificateur sommateur. La taille des pas et leur nombre seront déterminés par le nombre d’harmoniques combinées. Plus vous en utilisez, plus les étapes sont petites et nombreuses, meilleure sera donc l'approximation de votre forme d'onde originale. La détermination de ces coefficients de combinaison à partir de la forme d'onde souhaitée nécessite une considération un peu plus détaillée.
Synthèse de formes d'ondes
Avant d’approfondir les aspects théoriques des applications Walsh, un examen de ce que nous essayons de faire et la manière dont nous avons l’intention de le faire nous aidera à démarrer sur des bases solides. Le dispositif que nous souhaitons construire à l'aide des fonctions de Walsh pourrait être appelé "un convertisseur de forme d'onde carrée en forme d'onde arbitraire". Ce sera un circuit dans lequel vous insérez une onde carrée d'une certaine fréquence et d'où sort un signal analogique périodique avec une fréquence liée à celle de l'onde d'entrée (cela peut-être un sous-multiple) et une onde qui peut prendre n'importe quelle forme. Forme souhaitée en ajustant un ensemble de commandes, d'interrupteurs ou de résistances internes. Avec un tel appareil, la logique numérique pourrait être utilisée pour synthétiser une fréquence et le convertisseur pourrait ensuite être configuré pour produire une onde sinusoïdale destinée à être utilisée dans des applications standard, ou, avec une précision de conversion suffisante, un ordinateur pourrait être amené à parler ou même à chanter. Les deux ont été réalisés par des ingénieurs travaillant dans ce domaine. Le convertisseur se compose de deux parties : la première est l'expandeur numérique qui étend l'onde carrée d'entrée en une variété de formes d'onde numériques, et la seconde est le combinateur analogique qui additionne ces formes d'onde pour produire la sortie analogique périodique. L'expandeur est, bien sur, le générateur Walsh présenté précédemment et le combinateur sera discuté ci-dessous.
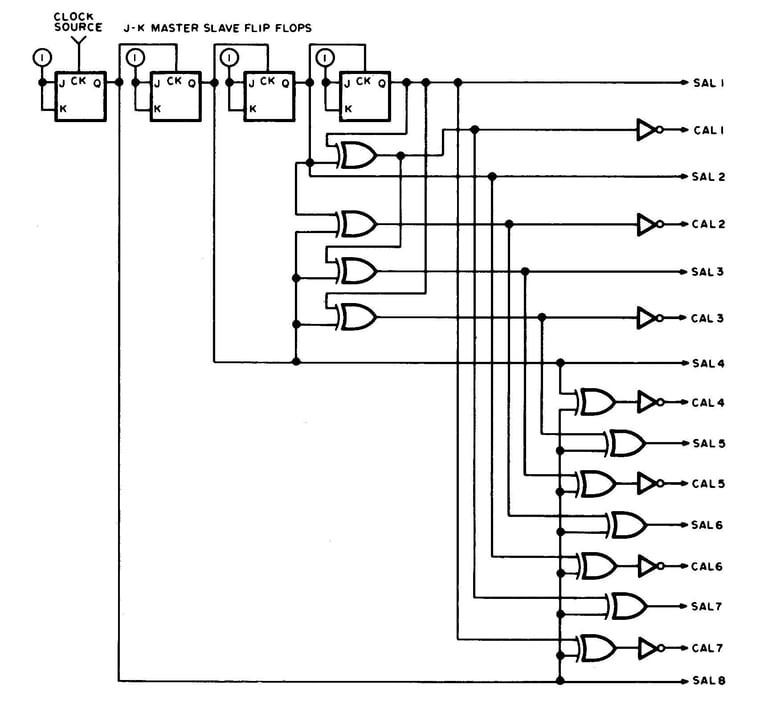
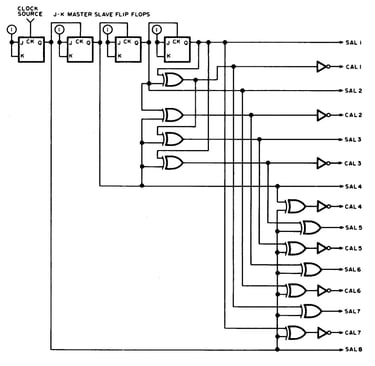
Figure 3 : En prolongeant la logique de la figure 2, ce circuit génère toutes les fonctions de Walsh WAL(1) à WAL(15) comme illustré sur la figure 1. Ce circuit utilise un autre type de bascule, le flip flop maître-esclave JK connecté comme bascule. Ce circuit pourrait être construit avec deux circuits intégrés 7473, trois circuits intégrés 7486 et un circuit 7404. (Une des 12 sections OU exclusives est utilisée comme inverseur)
Toutes les sorties Walsh seront introduites dans la jonction sommatrice d'un amplificateur opérationnel mais elles n'auront pas la même force ni le même signe. C'est la force et le signe de chaque composant qui détermineront la sortie analogique nette de sorte qu'une fois que nous avons choisi la sortie analogique souhaitée, la force relative et le signe de chaque harmonique de Walsh doivent être calculés à partir de la forme d'onde souhaitée. Une fois ces valeurs connues, un signe négatif peut être géré par un inverseur numérique et l'amplitude par le choix de la valeur de la résistance dans la jonction sommatrice. La sortie nette sera alors une approximation en escalier de la sortie souhaitée qui pourra ensuite être rendue plus parfaite par un filtrage passe-bas pour lisser la forme d'onde. Théoriquement, le calcul des coefficients à partir de la forme d'onde analogique souhaitée implique des opérations complexes avec les calculs d'intégrales mais il s'avère qu'il est possible de raccourcir les calculs en commençant non pas par le signal analogique, mais plutôt par la fonction d'approximation des marches d'escalier elle-même. Cette fonction peut être facilement déterminée à l’œil ou en prenant simplement la hauteur de chaque pas comme étant la valeur de la sortie analogique au centre de chaque intervalle de temps. La figure 4 montre deux exemples : une rampe linéaire et une onde sinusoïdale avec 16 approximations de pas. La hauteur de chaque pas est indiquée. Avant de procéder à un calcul proprement dit, nous donnerons quelques règles de gain de temps et de travail, illustrées dans la figure 5.
Quel est le résultat lorsque l'analyse de la fonction de Walsh est appliquée à une rampe linéaire ?
Un ensemble de valeurs de résistances qui forment un convertisseur DA (Digital/Analogique) ordinaire fonctionnant sur la valeur binaire du compteur utilisé pour le générateur de fonctions de Walsh.
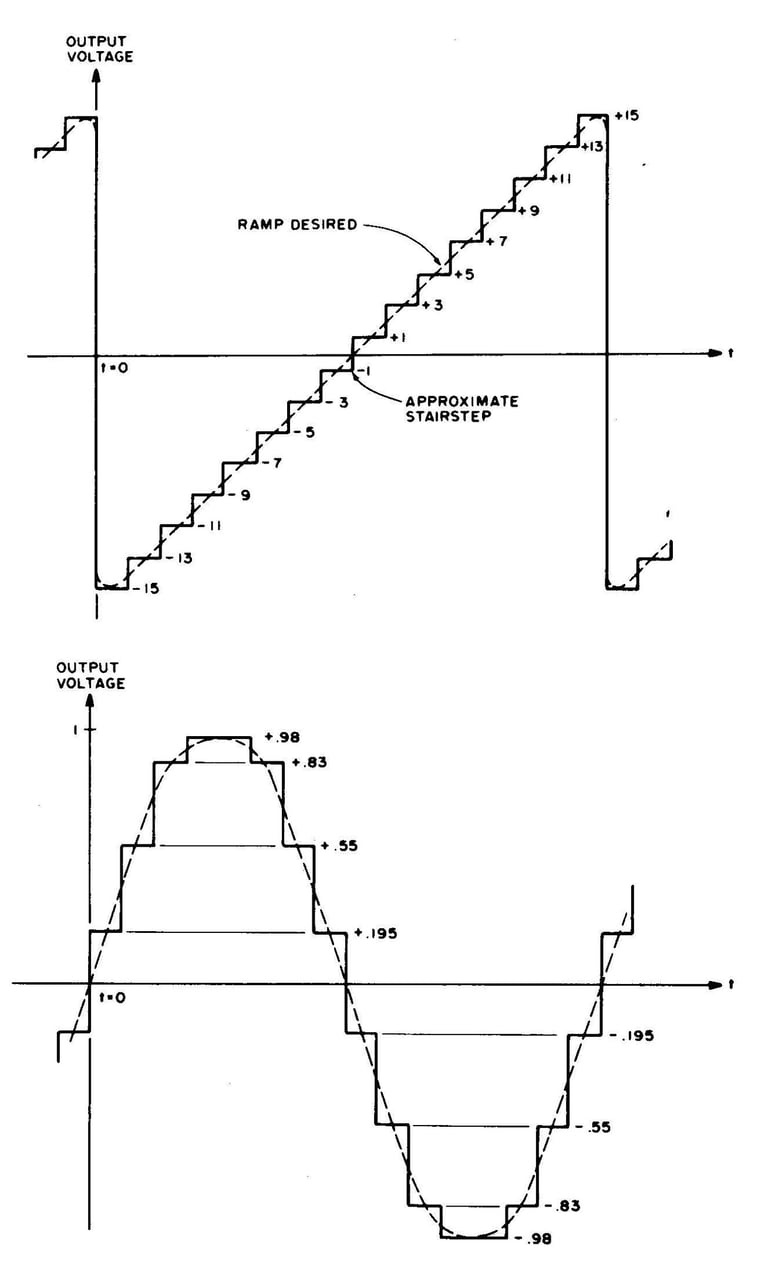
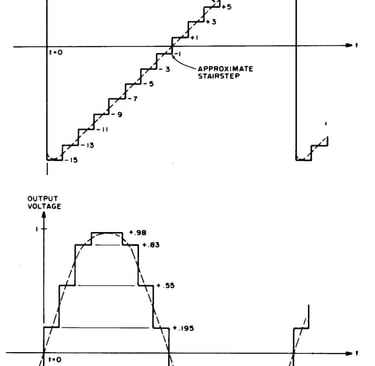
Figure 4 : En choisissant une série de constantes de pondération pour chaque terme de la fonction de Walsh, les sorties de la figure 3 peuvent être additionnées par un amplificateur opérationnel pour produire des formes d'onde arbitraires. Voici des exemples d'approximations d'onde en dent de scie et d'onde sinusoïdale générées par la méthode de la fonction de Walsh. La courbe lisse est celle souhaitée dans chaque cas, obtenue en filtrant la sortie de l'amplificateur sommateur.
1. La forme d'onde à synthétiser doit être répétitive (comme dans la synthèse de Fourier), bien qu'il soit facile de démarrer et d'arrêter à tout moment en contrôlant l'entrée numérique.
2. Il est particulièrement avantageux d'utiliser un nombre de pas multiple de n puissance 2 en une seule période car cela donne une coupure automatique du nombre d'harmoniques de Walsh requis. Ainsi : avec une sortie à 4 étapes, aucune fonction au-delà de WAL(3) n'est requise, avec une sortie à 8 étapes, aucune fonction au-delà de WAL(7) n'est requise, avec une sortie à 16 étapes, aucune fonction au-delà de WAL(15) n'est requise... etc.
3. Si les coefficients pour une approximation d'ordre supérieur sont calculés (disons 16 étapes) et qu'une approximation moins précise peut être utilisée (disons 8 étapes), il suffit alors de ne pas utiliser WAL(8) à WAL(15) puisque les coefficients d'ordre inférieur auront la même valeur dans les deux cas (ou presque). Cet effet est démontré dans le circuit générateur sinusoïdal. Si votre forme d'onde à synthétiser possède certaines symétries ou peut être amenée à le faire par un décalage de la ligne de base DC, de nombreux coefficients de composants de Walsh seront nuls, ce qui simplifiera non seulement les calculs, mais également les circuits.
4. Si la forme d'onde à synthétiser est paire, c'est-à-dire que toute valeur que prend la fonction à gauche du centre est la même que la valeur à égale distance à droite du centre, alors seules les fonctions CAL seront utilisées. et tous les coefficients SAL seront nuls.
5. Si la forme d'onde est impaire, ou peut être rendue telle par un décalage de la ligne de base, alors seules les fonctions SAL seront utilisées et tous les coefficients CAL seront nuls. Ici, toute valeur à gauche du centre est égale à moins la valeur à droite du centre.
6A. Si la forme d'onde est paire comme au point 4 ci-dessus et qu'elle est paire à environ 1/4 de cycle, alors seul CAL(k) où k est un nombre pair sera présent et tous les CAL(k) où k est un nombre impair seront à zéro.
6B. Si la forme d'onde est paire comme au point 4 et qu'elle est impaire à environ 1/4 de cycle, alors seul CAL(k) où k est un nombre impair sera présent et tous les CAL(k) avec k un nombre pair seront à zéro.
7A. Si la forme d'onde est impaire comme au point 5 ci-dessus et qu'elle est en outre paire à environ 1/4 de cycle, alors seul SAL(k) où k est un nombre impair sera présent et tous les SAL(k) où k est un nombre pair seront à zéro.
7B. Si la forme d'onde est impaire comme au point 5, et en plus impaire à environ 1/4 de cycle, alors seul SAL(k) avec k un nombre pair sera présent et tous les SAL(k) où k est un nombre impair seront à zéro.
Dans les calculs qui suivent on observera également que si une forme d'onde est paire ou impaire, les sommes signées des valeurs de pas ne doivent être calculées que pour la première moitié de l'onde puisque cette valeur sera exactement la moitié de la somme de toutes les valeurs. Cela se comprendra probablement mieux en examinant quelques exemples pratiques.
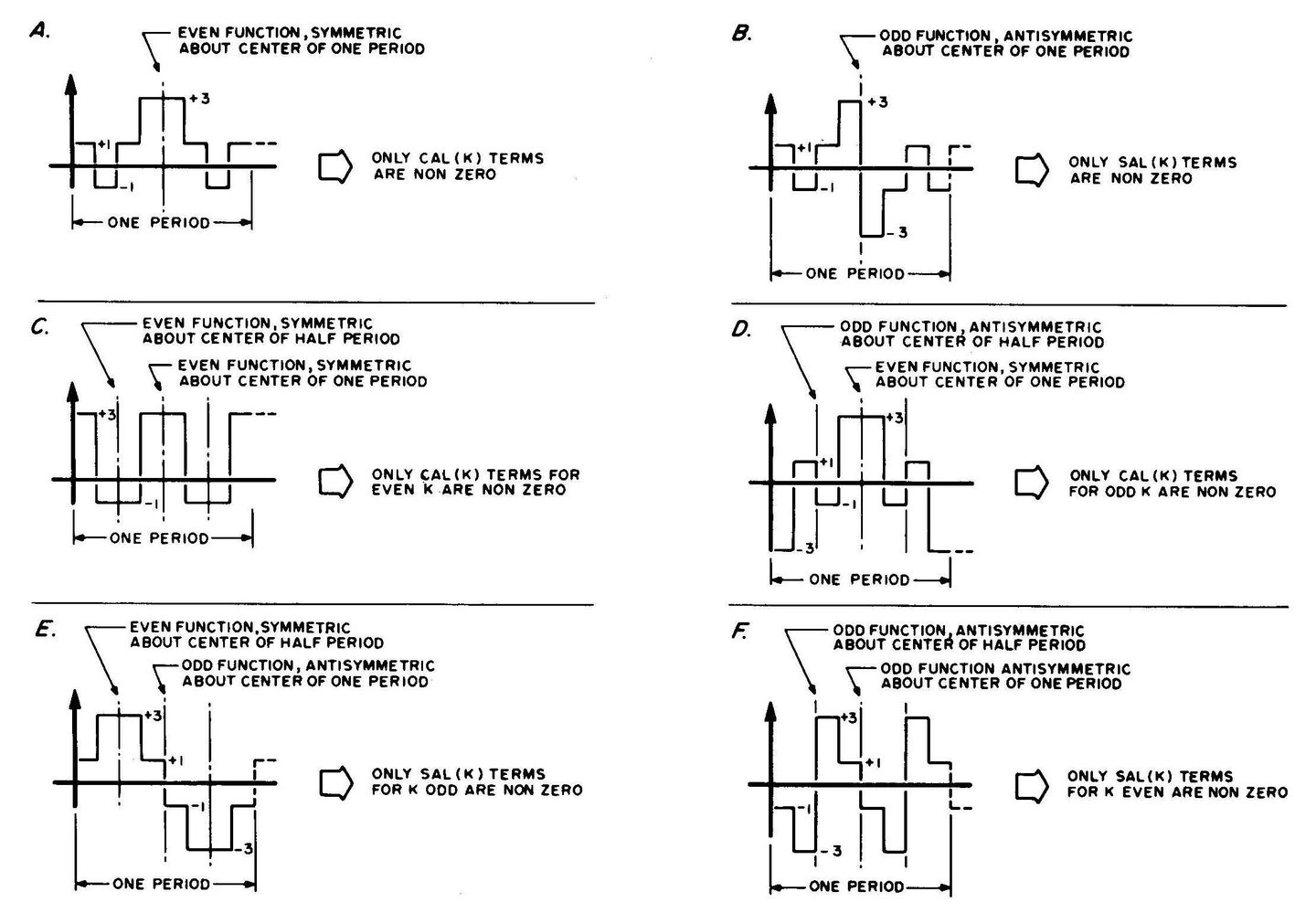
Figure 5 : Les propriétés des fonctions paires et impaires donnent des contraintes sur les constantes de pondération nécessaires pour une forme d'onde donnée. Voici les illustrations de six cas particuliers de symétries différentes qui donnent des termes nuls dans la somme de la fonction de Walsh. Pour rappel: even = pair, odd= impair, one period = 1 cycle.
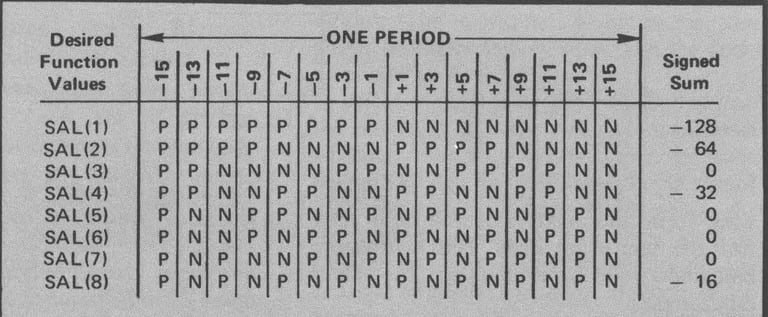
Tableau 2 : Un tableau de calcul utilisé pour aider à déterminer les coefficients de la fonction Walsh pour la forme dent de scie (rampe). La force relative du terme SAL ou CAL en question est obtenue en additionnant horizontalement la valeur de la fonction Walsh +1(P) ou -1(P) multipliée par la valeur réelle de la forme d'onde souhaitée pour cet élément de temps. Après avoir déterminé la valeur de la somme signée pour chaque terme, les valeurs doivent être normalisées de sorte que la plus grande grandeur soit 1 (quel que soit le signe). Les ratios normalisés indiqués ci-dessus ont été calculés en supposant que -128 correspondait à -1.
Signe des fonctions Walsh
P = Positif N = Négatif
SAL(1) = -1 = -1
SAL(2) = -0.5 = -1/2
SAL(4) = -0.25 = -1/4
SAL(8) = -0.125 = -1/8
Deux exemples:
Le premier exemple sera la rampe linéaire. Cette fonction peut être rendue impaire en ajustant la ligne de base, donc selon la règle 5 on voit que seuls les coefficients SAL doivent être calculés et qu'aucune fonction CAL n'a besoin d'être générée. La meilleure façon de bien réfléchir dans le calcul des coefficients est de créer un tableau comme indiqué dans le tableau 2. La valeur souhaitée pour chaque étape comprenant la fonction de sortie est écrite dans l'ordre en haut du tableau. Puisque nous essayons de produire une rampe linéaire, notre résultat sera un escalier montant avec une augmentation fixe à chaque marche (nous avons utilisé deux unités par marche). Cet escalier sera éventuellement filtré pour supprimer les défauts et donner une rampe linéaire. Le corps du tableau montre le signe (positif ou négatif) que prend chaque fonction de Walsh particulière dans chacun des 16 intervalles de temps dans lesquels une période de la forme d'onde de sortie a été divisée. Comme indiqué précédemment, nous n'avons pas besoin de dépasser WAL(15) dans ce cas. Les valeurs du signe de Walsh peuvent être tirées des formes d'onde de la figure 1 ou du tableau 3, qui convient jusqu'à 32 approximations de segments.
Les nombres à l'extrême droite sont les sommes des valeurs supérieures lorsque tous les signes sont pris en compte. Ainsi, pour WAL(1), nous voyons qu'il est positif dans la première moitié des cycles, mais les valeurs de pas sont négatives, nous obtenons donc :
(-15) + (-13) + (-11) + (-9) + (-7) + (-5) + (-3) + (-1) = -64 et dans la seconde mi-période où WAL (1) est négatif et les valeurs positives on obtient : -(+1) - (+3) - (+5) - (+7) - (+9) - (+11) - (+13) - (+15) = -64 soit un total de -128. Ce nombre donne la force relative de WAL(1) dans la sommation de sortie. Nous répétons le processus pour chaque fonction de Walsh.
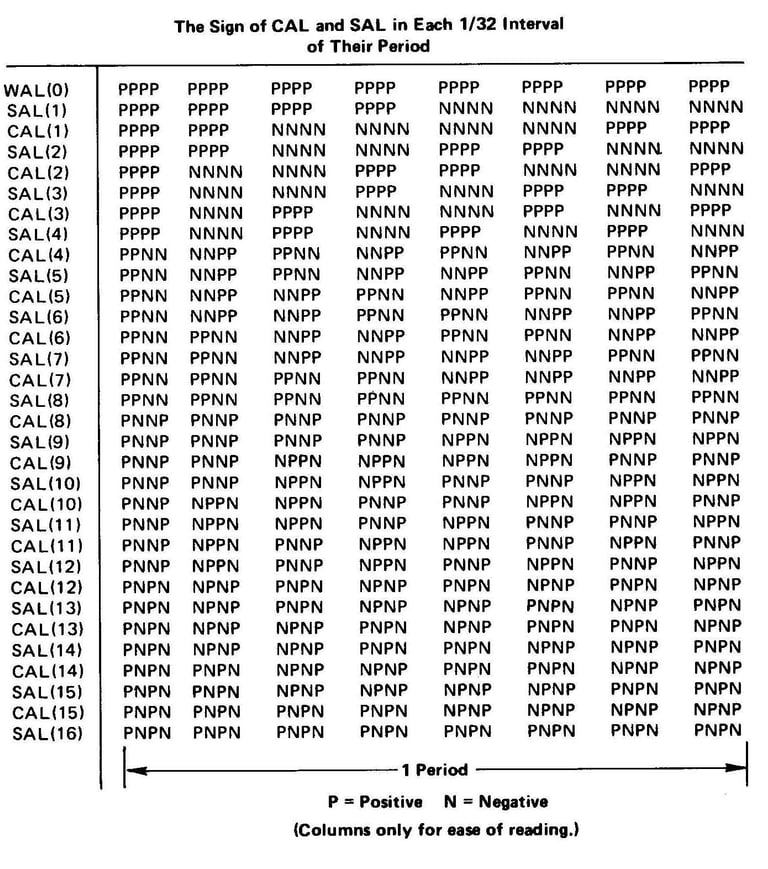
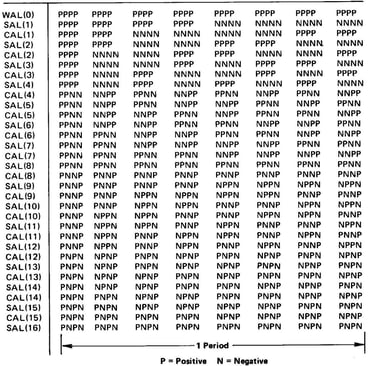
Tableau 3 : Un tableau de calcul plus grand donnant 32 composants de la fonction de Walsh et leurs signes sur une période de 32 intervalles.
Si l’on divise toutes les valeurs non nulles par la plus grande (WAL(1)), on observe que la pondération est binaire et également que seules les fonctions de Rademacher à onde carrée sont non nulles. Ainsi, on voit que la manière de générer une rampe consiste à utiliser un compteur alimentant un convertisseur digital/analogique standard. (Nous avons donc ici un chemin long et compliqué pour arriver à un résultat "évident", mais il convient également de noter que la pondération binaire D vers A ne "correspond" qu'à une sortie de forme rampe).
Si une autre forme d'onde telle qu'une onde sinusoïdale est souhaitée, un convertisseur A vers D peut être utilisé, mais une méthode plus précise consisterait à basculer entre 16 tensions de valeurs appropriées. Le système de Walsh est tout aussi précis et plus simple pour le cas plus général. Si nous divisons une onde sinusoïdale en 16 parties, la valeur au centre du premier intervalle sera Sin(11,25°) = 0,19509 et la suivante sera Sin(33,75°) = 0,83147, etc. Cela produit la rangée supérieure de notre tableau. Puisque Sin(x) est une fonction impaire, même autour de 1/4 de cycle, seuls SAL(1), SAL(3), SAL(5) et SAL(7) sont des valeurs de coefficient calculées, comme indiqué dans le tableau 4. Étant donné qu'un circuit de sommation d'amplificateur opérationnel standard (nous n'entrerons pas dans les détails ici car ils peuvent être trouvés dans n'importe quel livre sur les amplificateurs opérationnels), les rapports de sommation relatifs sont liés à l'inverse des valeurs de résistance de sommation, nous divisons chaque valeur normalisée en 1 et multiplions par la valeur de la résistance de rétroaction (feedback) pour obtenir chaque valeur de résistance de sommation en ohms. Le tableau 5 montre les valeurs calculées par rapport aux valeurs standard des résistances EIA de 1 % et 5 %.
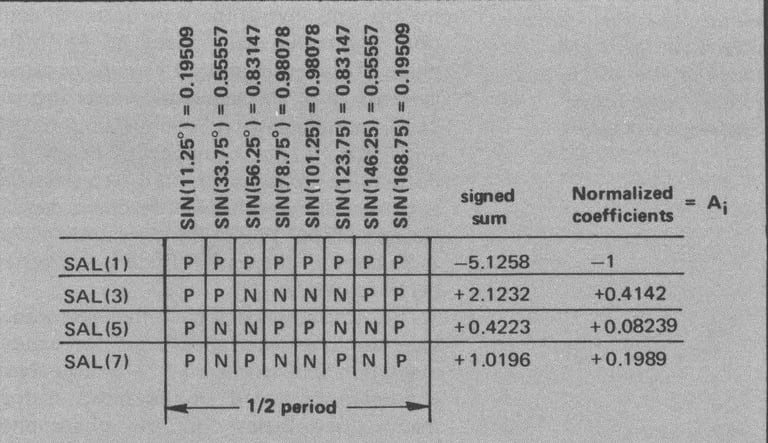
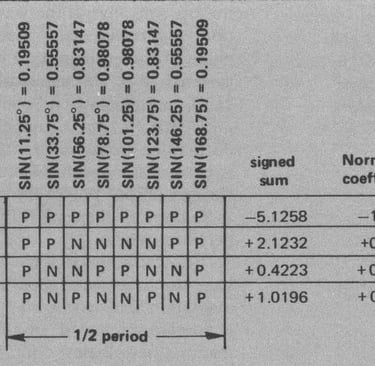
Tableau 4 : Utilisation du tableau informatique pour calculer les valeurs de résistance pour une approximation d'onde sinusoïdale en 16 étapes. Le générateur d'onde sinusoïdale spécialisé de la figure 6 utilise ces résultats, sous réserve d'une approximation supplémentaire indiquée dans le tableau 5. Notez que les signes des coefficients prennent en compte la configuration de l'ampli opérationnel inverseur et apparaissent donc inversés.
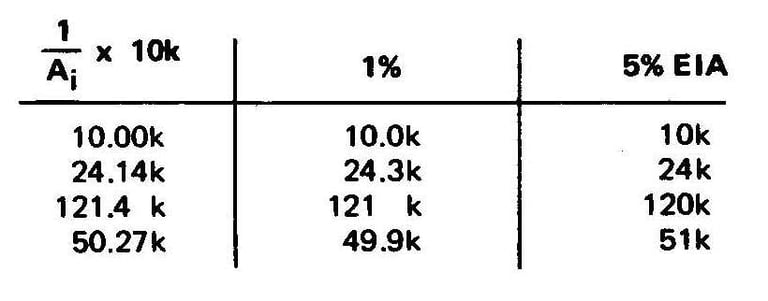
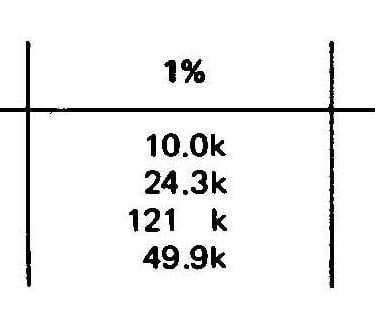
Tableau 5 : équivalents de résistance EIA pour les valeurs calculées du tableau 4. Les valeurs de résistance de 5 % de tolérance indiquées à droite ont été utilisées dans le circuit de la figure 6.
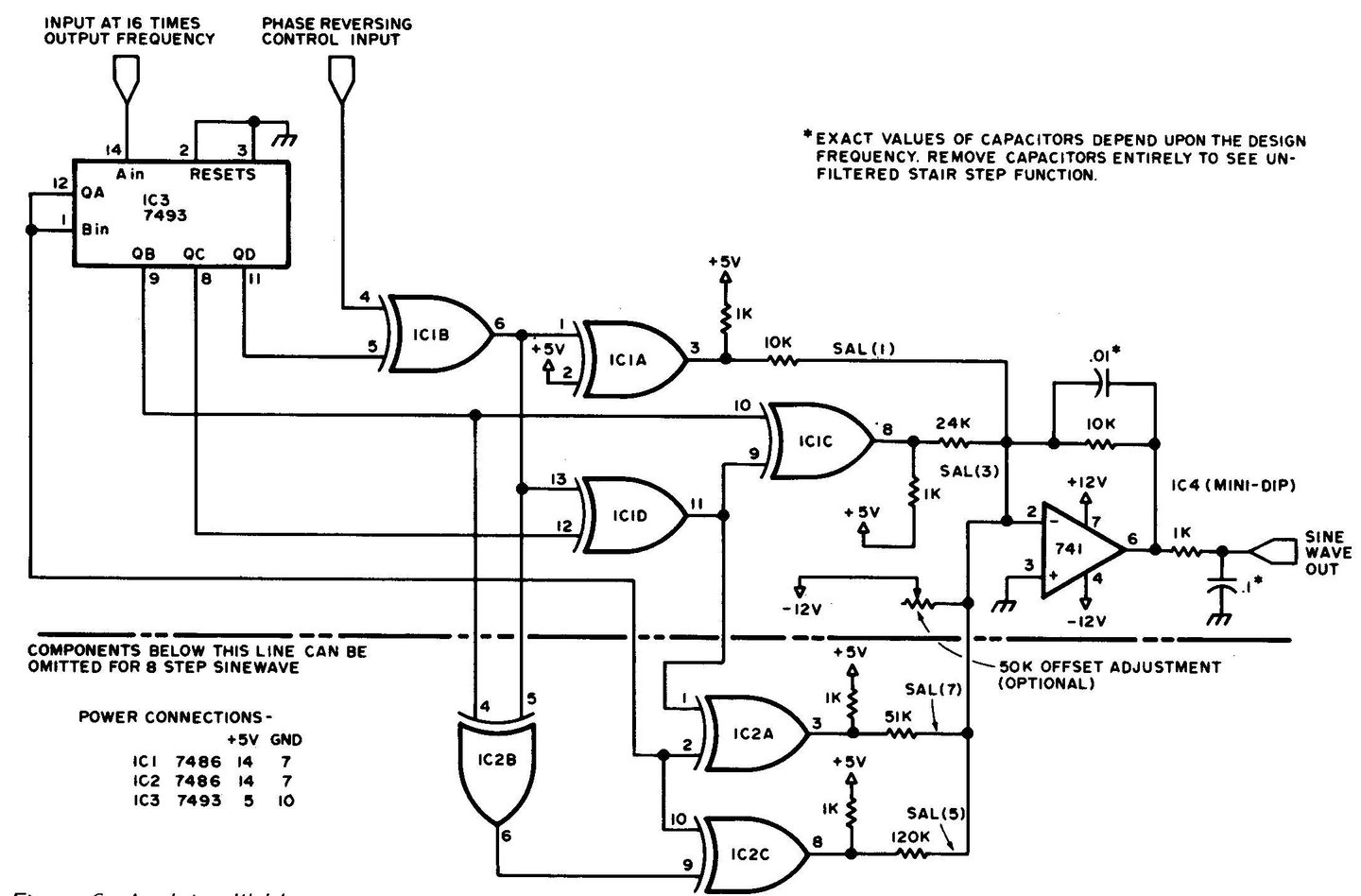
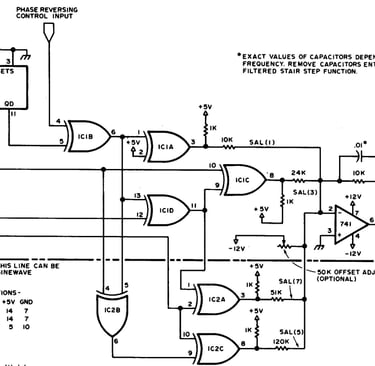
Figure 6 : Application des fonctions de Walsh. Voici le circuit d'un générateur d'onde sinusoïdale qui produit une approximation par fonction de Walsh de la fonction sinusoïdale. La fréquence de l'onde est définie par l'entrée de la broche 14 du 7493. Les composants de filtrage de l'amplificateur opérationnel aident à lisser la forme d'onde en escalier générée par la somme des composants de la fonction Walsh pondérés par les résistances.
Le circuit convertisseur sinusoïdal total est illustré à la figure 6. Alors que trois des coefficients étaient négatifs, un seul inverseur a été utilisé sur la seule sortie positive de Walsh puisque l'ampli opérationnel inverse la forme d'onde. De plus, une porte a été ajoutée grâce à laquelle la phase de la forme d'onde de sortie entière peut être inversée en inversant simultanément tous les composants de Walsh. Il est intéressant de noter également que si les composants situés sous la ligne pointillée sont supprimés, une approximation sinusoïdale en 8 étapes est obtenue. Le condensateur de rétroaction et le filtre passe-bas de sortie peuvent être ajoutés pour lisser la forme d'onde afin de donner une onde sinusoïdale presque parfaite.
Les méthodes Walsh présentées ici semblent avoir de larges applications pour l'expérimentation et l'ingénierie. Bien que ces concepts soient basés sur des mathématiques avancées, comme le philosophe Sénèque l'a observé il y a de nombreuses années, "le langage de la vérité est simple".
Fonctions Walsh pour la synthèse musicale ?
Certaines informations générales sur l'utilisation des fonctions orthogonales dans la synthèse des formes d'ondes musicales ont été générées par Hal Chamberlin et publiées dans Electronotes Newsletter, Volume 4, Numéro 25, du 20 juillet 1973. Hal a également envoyé une copie d'une partie d'un rapport de B. A. Hutchins, 60 Sheraton Dr, Ithaca NY 14850, sur l'utilisation des fonctions de Walsh dans un générateur de formes d'onde. Selon Hal, il y a eu une analyse considérable des fonctions de Walsh dans les cercles de musique électronique au cours d'une période approximativement centrée sur 1973, mais la complexité du contrôle numérique des amplitudes harmoniques de Walsh a conduit à la disparition de cet intérêt. L'approche actuelle de Hal consiste à utiliser un module d'évaluation de séries de Fourier en temps réel qui additionne numériquement les termes des 32 premières composantes d'une série de Fourier, spécifiés avec une précision de 8 bits en amplitude et en phase.
Glossaire:
Les termes suivants peuvent ne pas être familiers à certains lecteurs et sont mis en évidence avec des explications supplémentaires.
Base de référence: Il est possible d'ajouter un niveau DC fixe à un signal analogique, ce qui n'affectera pas sa forme d'onde. L'utilisation des niveaux 0 V et +5 V obtenus avec des circuits TTL (utilisant des résistances pull up) comme « fonctions de Walsh » correspond à un ajustement de base de +2,5 volts au cas idéal d'une valeur de tension symétrique positive ou négative.
CAL: Un acronyme dérivé de Cosine wALsh. Les fonctions CAL sont les fonctions de Walsh « paires », analogues aux fonctions cosinus de Fourier.
Cycle de service: pour une forme d'onde numérique, le cycle de service est le pourcentage de temps passé à l'état haut par rapport à la période complète de la forme d'onde.
Fonction paire: Une fonction paire (ou forme d'onde) est une fonction symétrique par rapport au point central de sa période, de son cycle. Cela signifie que sa valeur à une certaine distance à gauche du centre est la même que sa valeur à la même distance à droite du centre.
Fondamentale: la fréquence la plus basse dans une sommation de fonctions de Fourier ou de Walsh.
Code Gray: code binaire modifié de sorte qu'un seul bit change lors du passage au nombre immédiatement supérieur ou inférieur. Il est souvent utilisé pour désengager les codeurs de position.
Harmonique: Fréquence qui est un multiple de la fréquence fondamentale.
Calcul intégral: formalisme mathématique utilisé pour calculer l'aire sous une courbe. Le calcul intégral est utilisé conjointement avec la théorie des fonctions orthogonales pour évaluer analytiquement les coefficients des expansions des fonctions de Fourier et de Walsh. L'exemple de calcul des coefficients de la fonction Walsh dans cet article utilise les propriétés des fonctions de Walsh pour simplifier le processus de calcul des intégrales requises pour les coefficients. Il n'existe pas de telle simplification pour les coefficients de Fourier d'une forme d'onde, ce qui rend l'application de l'analyse de Fourier plus compliqué.
Fonction impaire: Une fonction impaire (ou forme d'onde) est une fonction antisymétrique par rapport au point central de sa période. Cela signifie que si à un intervalle fixe avant le point central sa valeur est X, alors au même intervalle après le point central, la valeur sera -X.
Fonctions orthonormales: La théorie mathématique des fonctions orthonormées est l’un des outils les plus puissants utilisés par les physiciens, les chimistes théoriciens et les ingénieurs. Entre autres applications, il fournit les outils nécessaires pour analyser des formes d'onde complexes et synthétiser ces formes d'onde en utilisant le principe de superposition. Que le tout est une somme linéaire de ses parties. Les séries de Fourier et l'analyse des fonctions de Walsh mentionnées ici sont deux choix particuliers d'un ensemble de fonctions orthonormées qui ont des applications pratiques utiles. (Voir également le spectre ci-dessous).
Forme d'onde périodique: Une forme d'onde périodique est une forme d'onde fixe qui se répète constamment. Un exemple simple serait le signal de l'oscillateur d'horloge d'un processeur central d'ordinateur maison typique. Un exemple plus compliqué (sous réserve d'imperfections) serait un son long et régulier joué sur un instrument de musique.
Fonctions Rademacher: le sous-ensemble des composantes de Walsh uniquement composé des ondes carrées non modifiées.
SAL: Un acronyme dérivé de Sine wALsh. Les fonctions SAL sont les fonctions de Walsh « impaires », analogues aux fonctions sinusoïdales de Fourier.
Séquence: terminologie de la fonction de Walsh faisant référence aux composantes de Walsh d'une forme d'onde exactement de la même manière que la fréquence est utilisée pour désigner les composantes de Fourier. Exemple : Spectre de séquence.
Spectre: Lorsque des fonctions orthonormées sont utilisées pour analyser une forme d'onde, le résultat est souvent un ensemble de coefficients qui pèsent chacune des fonctions de base trouvées dans une somme (théoriquement) infinie qui représente la forme d'onde. Chaque coefficient correspond à un paramètre des fonctions orthonormées, qui pourrait être, par exemple, un nombre "n". Quel que soit le paramètre, un spectre pour l'analyse est obtenu en traçant les valeurs des coefficients par rapport à la valeur du paramètre pour un grand nombre de coefficients. Pour une analyse de Fourier, le résultat est un tracé des coefficients par rapport à la fréquence (qui, à l'extrémité inférieure, correspond à une petite valeur entière). Un spectre de Walsh tracerait le coefficient de WAL(n) par rapport à n.
Forme d'onde: Pour cet article, la forme d'onde d'un signal est une valeur (par exemple) de tension en fonction du temps.


